ニュースレターNo.81/2022年7月発行

暗号技術から見る量子計算機のいま

1 はじめに

「量子計算機」という言葉をさまざまなメディアで見かけるようになって既に久しい。「量子計算機ができたら、今の暗号化通信技術は使えない」「量子計算機ができたらAIが進化する」などさまざまな情報が飛び交う中、そもそも量子計算機の現状がどうなっているか、また、量子計算機が出てくることで何がどう変化するのか、本号と次号の前後編に分けて執筆したい。なお、本稿では、量子計算機については数式を出さずに現状のみを説明する。詳細を知りたい方は、各所で引用している文献・記事を参照されたい。

2 量子計算機とは

おそらく大多数の人が持つ疑問が、節題のものだろう。その答えとしては「量子力学を応用したコンピュータ」がよく書籍では表現として用いられている。今一つ意味がわかるようでわからないこの表現がよく用いられる背景には、量子計算機は従来の計算機技術よりも物理学に依っていることが挙げられる。まず我々が普段利用しているパソコンやスマートフォンは「古典」計算機と呼ばれており、各データは電圧が「高い」あるいは「低い」という一つの物理的な状態に基づいて、 1ビットずつ表現される。これに対して量子計算機では、量子の状態に基づいて、量子ビットと呼ばれる情報で表現される。まず量子の世界では、量子がどの方向を向いているかで状態を表現する。これは古典計算機で言うところの「高い」状態と「低い」状態以外にも、さまざまな状態が表現できることを意味する。

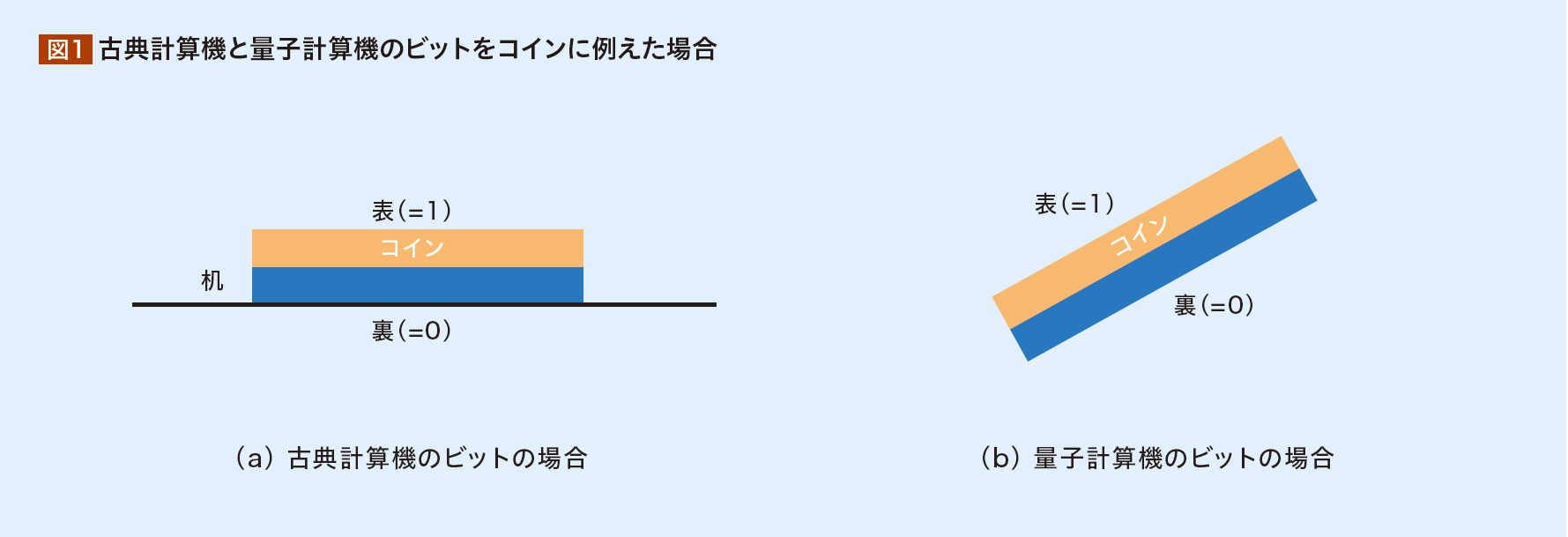
古典計算機のビットと量子計算機の量子ビットの違いとして、個人的にもっともわかりやすい例えだと思うのは、 CRYPTO 2017の招待講演^※1でカリフォルニア大学サンディエゴ校のJohn Martinis先生が話していたコインで考えた場合である。古典計算機におけるビットは「机の上に置いたコイン」であり、表か裏という状態しか持たない。これに対して量子計算機における量子ビットは「空中に浮かんでいるコイン」であり、さまざまな傾斜を持たせることであらゆる状態を持たせることが可能となる。図1がそのイメージである。図1-(b)の例ではコインがどちらを向いているかにより、表・裏の表現以上の状態を表すことができる。図における各コインがそれぞれの計算機におけるビットに対応するとして、ビット数が増えることで計算機が表現できる情報が指数関数的に増加する。これが量子計算機は高い計算能力を持つと考えられている直観である。なお、古典計算機でできる計算は、量子計算機でも実現できることは想像に難くない。詳細な原理については日本語でも多くの書籍が出版されているので、それらにお任せしたい。

※1 John Martinis, “Prospects for a Quantum Factoring Machine,” Invited talk, CRYPTO 2017.

ところで、量子計算機は前述した通り物理学に強く依存している。実際に研究者も物理学の研究者と情報学の研究者がおり、著者の認識では、物理学の研究者が量子の特性に基づいて計算機そのものを開発し、情報学の研究者が実際に計算機の内部で走る計算論理を研究しているように見受けられる。つまり、量子計算機の発展には情報学の研究だけではなく、物理学の研究も欠かせない。コインの例を解説していたJohn Martinis先生も物理学が専門である。この量子計算機が物理学と情報学の双方の上で成り立っている観点は、情報技術そのものが他の学問と融合する学際領域になっている証拠と考えている。

3 ショアのアルゴリズム

冒頭でも記載した「量子計算機ができたら今の暗号化技術は使えない」ということも、メディアなどではよく取り上げられる話である。著者が考えるに、おそらくこれは量子計算機が注目されているもっとも重要な理由だろう。では、なぜ「量子計算機ができたら今の暗号化技術は使えない」という認識がされるに至ったのか？

結論から言えば、「ショア（Shor）のアルゴリズムがあるから」である。論文に記載される表現で言うなら、1994年にショアという研究者が、量子計算機があれば素因数分解問題と離散対数問題が多項式時間で求解可能であることを発見した^※2。ここで言う多項式時間とは「現実的な時間」と思ってもらいたい。素因数分解問題はRSA暗号が、離散対数問題はDHEなどがそれぞれ安全性の根拠とする問題であり、「これらの問題を多項式時間で解くことができない」という仮定がRSA暗号やDHEの安全性には必要だった。しかし、ショアのアルゴリズムによると、「素因数分解問題や離散対数問題が現実的な時間で解けてしまう」ことになるため、そもそも安全性の根拠が成立しない。つまり、量子計算機を用いることで、「公開鍵から秘密鍵を暴かれてしまった」「暗号文から平文を復号できてしまった」などが具体的な現象として発生する。なお、ショアのアルゴリズムは楕円曲線上の離散対数問題へも拡張がされており、 ECDSAやECDHEなどの安全性も破綻させることができる。これにより、大規模な量子計算機を作ることで現在使われている公開鍵暗号方式が破られることになるのである。

※2 Peter Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proc. of FOCS 1994, pp. 124-134, 1994.

ショアのアルゴリズムは、発表された当時、理論的な面からは世の中に大きな影響を与えた。その理由は大きく二つある。一つは公開鍵暗号の安全性が破れること、もう一つは現実の問題に対して量子計算機を導入することによる利点が初めて示されたことである。前者はいま世の中で量子計算機が注目されている理由そのものだが、後者の内容も興味深い。ショアのアルゴリズムが出てくる以前は人工的に用意した問題でしか量子計算機の効果は示されておらず、量子計算機を研究する意味が薄かったことが伺える。

その一方、ショアのアルゴリズムが発表された当初、世の中の暗号技術に与えた影響は、実は大きくなかった。当時は実際に動作する量子計算機が存在しなかったこと、また、実際に暗号で扱われる問題を解くには極めて大規模な量子計算機が必要だったためである。率直に言えば、「机上の空論」にとどまっており、世を席巻するには至らなかった。ショアのアルゴリズムが極めて重要なものとして世の中に脚光を浴びるのは、その発表から20年以上経った2010年代半ばの頃である。近年に至り数桁の計算なら実際に行える量子計算機のプラットホームが登場したことで、ショアのアルゴリズムの持つ価値が本当に重要なものとして認識されるようになった。 2016年には米国のNIST(米国国立標準技術研究所)が量子計算機に対しても安全性を保証できる暗号、すなわち耐量子計算機暗号を選定するプロジェクトを進めている。我が国においても総務省プロジェクト「安全な無線通信サービスのための新世代暗号技術に関する研究開発」を立ち上げるなど、その勢いが伺える。(耐量子計算機暗号については次回に解説したい。)

4 いまある量子計算機

IBM社は2016年に世界初となるクラウド型量子計算機を公開した。これは5量子ビットの計算が行える計算機だったが、 2017年5月に発表されたIBMQ (https://quantum-computing.ibm.com/) は16量子ビットの計算が行えた。 IBM社は2021年11月には127量子ビットの量子計算機を発表し、 2023年には1121量子ビットを持つ量子計算機を開発する予定である^※3。

※3 National Academies of Sciences, Engineering, and Medicine, “Quantum computing: progress and prospects,” National Academies Press, 2019.

ところで、IBMQは、クラウドとして誰もが利用できる量子計算機として公開されている。 IBMQはIBM Quantum Experienceのアカウントを作り、オープンソースの量子計算ソフトウェアキットであるQiskit (https://qiskit.org/）を導入することで利用できる。 Qiskitのユーザーは世界で30万人を超えている。現在は研究段階にある量子計算機だが、今後技術革新が進むにつれ、古典計算機を上回ることが期待されている。なお、QiskitはPythonでインストールパッケージが提供されており、 Pythonユーザーの方は、ぜひインストールしていただきたい。

著者も本稿の執筆を始めてから知ったことであるが、 Qiskitのハッカソンも行われているようである。ハッカソンとは与えられたテーマに沿って、限られた開発期間内でプログラミングを行うイベントである。 IBM社は2019年に量子計算機に関する合宿型ハッカソンを行っている。詳細は文献^※4を参照されたいが、日本ではQiskit Camp Asiaとして2019年11月18日に山梨県で学生および研究者を集めて行っている。また、量子計算機を使ったプログラミングコンテストとしてIBM Quantum Challenge (https://challenges.quantum-computing.ibm.com) もある。これらのコンテストでは演習問題を与えられ、その解法となるプログラムを構成することとなる。量子計算機に触れてみたい、雰囲気を感じたいという方は、ぜひこれらの機会も積極的に活用いただきたい。

※4 小林有里, 松尾惇士, 沼田祈史, “面白いぞ量子技術：9．量子コンピュータハッカソン -コミュニティによる量子人材育成-,” 情報処理学会誌, 62巻4号, pp.e53--e58, 2021.

5 実際に暗号は破れるのか

さて、実際に触れる量子計算機があるということで、読者の中には「暗号技術は破られるのか」という疑問を持つ方もいるかと思う。 CRYPTRECのレポート^※5によると、これまでに量子計算機で計算できた例は15の素因数分解のみである。素因数分解問題はRSA暗号の安全性の根拠となる問題であるが、今のRSA暗号で使われている素因数分解問題は600桁以上の数であり、暗号技術を破ったとは言い難い。 John Martinis先生のCRYPTO 2017の招待講演によると、現在RSA暗号で使われている2048ビットの素因数分解をするために必要な量子計算機の規模は、北米大陸4分の1程度の大きさとなる計算機を、10年間実行し続けることで可能となる。この実行コストは金額にして100京ドル(約1垓円)であり、消費電力量は1エクサワット(テラワットの100万倍)になる。これは例えば、地球全体で消費される電力1日分に相当するという。何とも冗談みたいな数字である。この数字のインパクトがあまりにも強いおかげで、著者自身にとっては忘れられない知識となった。なお、2021年時点の予測^※6では「拡張性のある量子計算機の時間軸を予測できるようになるには、時期尚早」と述べられている。結論を言うと、量子計算機の発展は目覚ましいものの、少なくとも暗号の安全性を脅かすにはまだまだ先の未来である。

※5 高安敦, “Shorのアルゴリズム実装動向調査,” https://www.cryptrec.go.jp/exreport/cryptrec-ex-3005-2020.pdf.

※6 National Academies of Sciences, Engineering, and Medicine, “Quantum computing: progress and prospects, ” National Academies Press, 2019.

余談であるが、量子計算機と暗号の関係性については、筑波大学の國廣先生の解説^※7が最もわかりやすい。数式をほとんど用いずに量子計算機と暗号の現状を解説しており、興味を持たれた読者はぜひ参照していただきたい。

※7 國廣昇, “量子計算機と暗号：耐量子計算機暗号への移行,” 日本セキュリティ・マネジメント学会誌, 35巻3号, pp. 18-24, 2022.

6 最後に

量子計算機に関する著者の知識について本稿には記載した。最後に著者の思いのたけをつづる。現在の暗号技術を破るような量子計算機の登場はまだまだ先であることは述べたが、その一方で量子計算機に対して安全な暗号技術、耐量子計算機暗号の検討はやはり精力的に取り組むべきだろう。いずれどこかでブレイクスルーが起きて、量子計算機の画期的な能力向上が起きることもあり得る話である。前述した通り、耐量子計算機暗号は我が国においても研究開発が盛んであり、国主導のプロジェクトなども展開されている。米国のNISTが進めている耐量子計算機暗号も最終ラウンドを迎えるなど、世界的な対策が進んでいるが、これらの内容については次回のインターネット10分講座で紹介したい。

(大阪大学大学院情報科学研究科矢内直人)

※ 著本の研究は、総務省の「電波資源拡大のための研究開発（JPJ000254）」における委託研究「安全な無線通信サービスのための新世代暗号技術に関する研究開発」の成果として実施されている。