ニュースレターNo.82/2022年11月発行
耐量子計算機暗号とは
1 はじめに
量子計算機は、 現代の社会において最重要と言って差し支えない研究領域である。 本稿は前号(No.81)のインターネット10分講座「暗号技術から見る量子計算機のいま」の続きであり、 前回の講座では、 量子計算機が実用化された際にはRSA暗号など従来の暗号技術が使えなくなること、 また、量子計算機の研究がどのような現状にあるかを紹介した。 本稿では、量子計算機が実用化されたあとでも、 安全性を保証する技術として注目されている「耐量子計算機暗号」の現状を解説する。 前号同様に耐量子計算機暗号について数式を出さずに現状のみを説明するため、 詳細を知りたい方は各所で引用している文献・記事を参照されたい。
2 耐量子計算機暗号とは
まず、耐量子計算機暗号の概念について述べたい。 耐量子計算機暗号は、一般に「量子計算機が実用化されても、 安全性を保つことができる暗号技術」として知られている。 厳密には、耐量子計算機暗号は「量子計算機にも安全性が示されている」暗号ではなく、 「量子計算機による効率的な解析方法が知られていない」暗号となる。 前号では、「ショア(Shor)のアルゴリズム」により、 現在の暗号技術が効率的に解かれてしまうことは述べた。 ショアのアルゴリズムは、 本稿執筆時点ではまだ現実的な脅威とはなっていないものの、 暗号技術の本来の役割に鑑みると、 安全性が損なわれる前に対策がなされることが望ましい。
詳細は次節で述べるが、耐量子計算機暗号は、 その安全性の根拠となる問題に基づいて分類される。 興味深い点は、いくつかの代表的な方式は、 ショアのアルゴリズムが発見された1994年よりも前に提案されていることである。 これらの方式は、公開鍵暗号の概念が初めて登場した1974年から、 公開鍵暗号の具体的な構成を求める中で提案されてきた。 一方、現在最も発展している暗号技術は、 ショアのアルゴリズムが登場した以降の1997年に提案された、 格子暗号と呼ばれる方式である。以降では、これらの暗号方式について、 全体像を説明する。 なお、耐量子計算機暗号の基礎知識については九州大学・縫田光司先生の書籍「耐量子計算機暗号」※1が日本語での専門書として出版されている。
3 耐量子計算機暗号の代表的な枠組み
前述した通り、 耐量子計算機暗号は安全性の根拠となる問題に基づいて提案されている。 既存の主な方式は格子暗号、符号ベース暗号、多変数公開鍵暗号、 同種写像暗号の四つである。 以下では、最も発展している暗号技術として格子暗号の詳細を述べる。 符号ベース暗号、多変数多項式暗号、 同種写像暗号については概要のみを述べる。
3-1 格子暗号
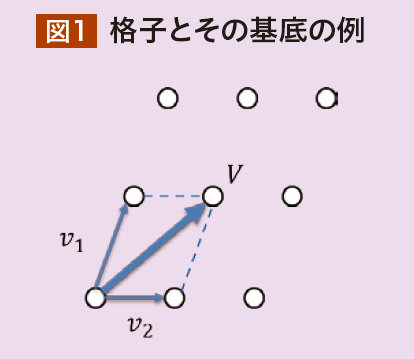
格子暗号は、高次元の格子に基づく公開鍵暗号技術である。 格子暗号は、 耐量子計算機暗号としての有望さが最も期待される暗号技術であり、 量子計算機に対して安全であることに加えて、 さまざまな利点を有している。 ここで言う格子とは大まかには、 実数上に定義される一次独立なベクトルによって表される集合として定義される。 また、そのベクトルを基底と呼び、各基底が持つ要素数を次元、 基底の数を階数と呼ぶ。 これだけだと何だかよくわからない読者が多いと思うので、 図1に例を示す。 図1で表される全体が格子であり、 図中のベクトルv_1, v_2が基底となる。 また、図1では次元と階数はいずれも2となる。 格子暗号で最もよく知られる問題である最短ベクトル問題(Shortest Vector Problem, SVP)は、格子の基底v_1, v_2が与えられた状態で、 そこから計算される最短ベクトルVを計算する問題である。 図の例は2次元ベクトルであるため簡単に思われるが、 これらのベクトルが存在する空間が3次元あるいはより高次元になった場合、 および、基底の数を増やした場合をそれぞれ考えてもらいたい。 この時、さまざまな方面を向いた多数のベクトルが散見される状態となり、 最短ベクトルの計算が複雑になることが想像できるだろう。 この難しさが格子暗号の安全性の根拠となる。
興味深いことに、 格子暗号は量子計算機に対する安全性を持つことに加え、 二つの利点を持つ。 まず、従来の暗号技術よりも高機能な暗号技術の実現が可能な点である。 その代表的な例が準同型暗号と呼ばれる、 暗号文に対する何らかの操作によって復号することなく、 中身の平文に対する操作が行える暗号技術である。 準同型暗号は、 データの秘匿性を満たしたままデータ操作が可能な技術として、 昨今ではデータ提供者のプライバシーを保障したAIの学習機能などへの応用が期待されている。 公開鍵暗号の歴史としては、 暗号文の操作から平文の積あるいは和を計算できる方式が知られていたが、 平文の和と積の両方を実現する準同型暗号、あるいは、 平文に対する任意の関数を計算できる準同型暗号(完全準同型暗号と呼ばれる)は、 公開鍵暗号が登場した1970年代から未解決問題として知られていた。 この30余年の未解決問題が、 2009年にクレイグ・ジェントリーによって解決された※2。 このジェントリーの方式はもちろん、 既存の完全準同型暗号は格子に基づいている。 直観的には、従来の暗号が剰余演算による整数であることに対し、 ベクトルとして定義される高次元の数学的概念を導入したことで、 より複雑な計算が可能になったと言える。 もう一つの利点は、高速性にある。 実は、格子暗号はRSAや楕円曲線に代表される暗号技術より高速である。 一つの例として、格子暗号の実装結果※3を表1に示す。 文献※4の著者らは格子暗号のライブラリを開発し、 RSAおよびECDHとその性能を比較評価している。 表に示す通り、 格子暗号は従来の暗号技術と比べて100倍以上の高速性を持つ。 すなわち、格子暗号の実装を推し進めることは理論的な安全性に加えて、 スループットの改善という実用面からも有益と言える。
| 方式 | 128bit | 256bit |
|---|---|---|
| RSA | 310回/秒 | - |
| ECDH | 5,930回/秒 | 1,610回/秒 |
| 格子 | 1,020,000回/秒 | 508,000回/秒 |
3-2 符号ベース暗号
符号ベース暗号は、 ショアのアルゴリズム登場前から存在する暗号技術であり、 誤り訂正符号に基づいて構成される。 ここで言う誤り訂正符号とは、 元は通信技術の信頼性を保証する技術として情報理論分野で提案された。 誤り訂正符号とは大まかには、 送信者が何らかの通信路を介して受信者にデータを送信する際、 その一部がノイズなどで変化しても、 高い確率で元のデータに復元する技術である。 誤り訂正符号の詳細は割愛するが、この時誤り訂正符号では、 誤りが訂正できるような何らかの数学的構造を用意する。 その構造に対するある種のランダムな変換を施すことで、 元のデータの特徴が隠されたような別の構造が生成できる。 この時、そのランダムな変換を秘密にできたならば、 変換後の構造から元のデータの構造を計算できないことが予想される。 これが符号ベース暗号の直観である。 初めて提案された符号ベース暗号は、 1978年のマクリース(McElice)暗号である。 誤り訂正符号そのものが複雑であることから本稿では詳細は割愛するが、 この方式が登場して40年以上経つものの、いまだに破られていない。 このため、安全性は高く信頼できると言える。 一方で、 符号ベース暗号はディジタル署名方式において効率的な構成が知られていない。 符号ベースのディジタル署名は、提案されては、 その安全性の問題が指摘されている。
3-3 多変数多項式暗号
多変数多項式暗号は、 多変数多項式からなる連立方程式の困難性を安全性の根拠とする暗号技術である。 直観的には多変数の連立方程式の解は、 一意に定まらないことが根拠となる。 多変数多項式暗号も、 ショアのアルゴリズム以前から存在していた暗号技術である※5。 なお、多変数多項式暗号では一般に二次の多項式を用いる。 多変数の連立二次多項式の解を計算する問題は、Multivariate Quadratic(MQ)問題と呼ばれる。
多変数多項式暗号の評価にはMQ問題の困難性だけではなく、 具体的なパラメータに対する計算量の評価も重要となる。 この評価に対してMQ問題を解答するコンテスト”Fukuoka MQ Challenge”(https://www.mqchallenge.org/)が、 2015年4月より開催されている。 名前から想像される通り、これは我が国発祥の評価であり、 福岡に拠点を置く九州大学と九州先端科学技術研究所の研究者が中心に企画していたことが名前の由来である。 MQ問題の主なパラメータとしては変数の個数、方程式の個数、 および方程式の係数が定義される体の種類が挙げられる。 Fukuoka MQ Challengeでは、 本稿を執筆している2022年9月時点では変数の個数や方程式の個数に応じてType IからType VIの6種類が定義されており、 近年では2020年8月に台湾のBo-Yin Yang教授のチームによってType IIIの変数38個、方程式76個の場合が解かれている。 2022年1月に各Typeにおいて新たなチャレンジが追加されたが、 本稿執筆時点では解いた報告はされていないようである。 これらの評価は、 多変数多項式暗号において今後も継続評価されるべき重要課題と言えるだろう。
3-4 同種写像暗号
同種写像暗号は上述した耐量子計算機暗号のうち、 最も新しく登場した暗号技術である。 これはECDH(楕円曲線ディフィー・ヘルマン鍵共有)などの基盤となる楕円曲線に対し、 同種写像と呼ばれる写像を用いた暗号技術である。 従来の楕円曲線暗号が単一の曲線における点の動きを考えることに対し、 同種写像暗号では複数の楕円曲線同士の関係を考える点が異なる。 楕円曲線暗号も詳細に述べると高度な数学的知識が必要となるため詳細は割愛するが、 多くの教科書が出版されており、 例えば大阪大学・宮地充子先生の書籍※6がある。
さて、 同種写像は楕円曲線から楕円曲線への写像の一種であることは先にも述べたが、 実は同種写像の概念は公開鍵暗号の概念よりも先に存在している。 例えば同種写像に関する有名な結果として、 1971年にベルーの公式(Velu’s formula)※7が示されている。 ベルーの公式の詳細は割愛するが、その証明としてまず同種写像を選び、 それに合わせて値域となる楕円曲線を求めている。 これに対し、二つの楕円曲線が与えられた状況で、 それらの楕円曲線を結びつける同種写像を求める問題は、 同種写像問題と呼ばれ、同種写像暗号の安全性の根拠となっている。 代表的な手法としては、鍵共有方式であるSIDH※8が知られている。
4 耐量子計算機暗号の現状
アメリカ国立標準技術研究所(National Institute of Standards and Technology, NIST) は、 2016年から耐量子計算機暗号に関する標準化規格の選定を進めている (https://csrc.nist.gov/projects/post-quantum-cryptography)。 2022年7月には暗号方式として一つの方式が、 ディジタル署名として三つの方式が標準化対象として選ばれたことが報道されてい る※9。 選ばれた方式は暗号化方式としてCRYSTALS-KYBER、 ディジタル署名としてCRYSTALS-Dilithium, F ALCON, SPHINCS+である。 また、上記の四つの方式とは別に新たなラウンドとして、 暗号化方式としてBIKE、Classic McEliece、HQC、 SIKEの四つの方式が標準化規格の候補として継続議論されている。 加えてディジタル署名方式が特に数に乏しいなどの理由もあり、 (本稿執筆時点では)2022年10月1日までさらに新たな候補の提出も受け付けている。
上記の方式において前節で述べた種類で分けると、 標準化されるものではCRYSTALS-KYBERとCRYSTALS-Dilithium、 FALCONが格子暗号、 SPHINCS+がハッシュベース署名(本稿では割愛する)である。 また、まだラウンドに残っているものとして、BIKE、Classic McEliece、HQCが符号ベース暗号、SIKEが同種写像暗号である。 格子暗号が多く、 それ以外の方式がまだ発展途上にあることがこの結果から伺える。 この実質的に格子暗号しか現状では標準化が決まっていないことが、 新たなラウンドが追加された背景にはある。 もし仮に格子暗号に有効な量子計算機のアルゴリズムが発見された場合、 かつてショアのアルゴリズムが発見された時以上の衝撃が世の中に発展する可能性が高いためである。 なお、選定の途中で標準化候補から外れてしまった方式には、 安全性上の問題が見つかっている方式も多い。 符号ベース暗号のディジタル署名などが、 安全性上の問題が見つかった代表的な例と言える。
ところで、上述した計8個の方式は、既存の暗号ライブラリliboqs (https://github.com/open-quantum-safe/liboqs) にも実装されている。 興味のある読者に向けたベンチマークとして、 liboqsを用いて計測した各方式の性能を表2、表3にそれぞれ示す。 これらの表においては、public keyが公開鍵のバイトサイズ、 secret keyが秘密鍵のバイトサイズ、 ciphertextあるいはsignatureが暗号文あるいは署名のバイトサイズにそれぞれ相当する。 また、計算時間はkeygen/sが毎秒あたりの鍵生成回数、 encaps/sあるいはsign/sが毎秒あたりの暗号化回数あるいは署名回数、 decaps/sあるいはverify/sが毎秒あたりの復号回数あるいは検証回数である。 これらの性能はUbuntu 18.04.6 LTS(Bionic Beaver )上で、 Intel® Core™ i7-8700K CPU 3.70GHzを搭載した32GBメモリを持つマシン上で計測した。 コンパイラはgcc 8.4.0を用いている。
まず暗号化方式について、 CRYSTALS-KYBERはKyber512とKyber768いずれも同種写像暗号によるSIKEを除く他の方式と比べて各バイトサイズと計算時間のバランスが取れているように見受けられる。 特に毎秒あたりの暗号化回数と復号回数の数値が高く、 これらが標準化されたことは順当に思える。 BIKEが継続して審議されていることも同様である。 一方、ディジタル署名は、 ハッシュベース署名であるSPHINCS+は公開鍵と秘密鍵のバイトサイズが小さいものの、 署名のサイズが大きくなっている。 FALCONは署名回数の数値が高いものの、検証回数の数値が低い。 これに対しCRYSTALS-Dilithiumは、 バイトサイズと計算時間のバランスが取れている。 このため、CRYSTALS-Dilithiumが総合的にみて最も優れているようにみえる。 耐量子計算機暗号の研究開発では、 これらの計算時間をいかに改善するかが議論されている。
https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4
| Algorithm | public key | ciphertext | secret key | shared secret key | keygen/s | encaps/s | decaps/s |
|---|---|---|---|---|---|---|---|
| BIKE-L1 | 1541 | 1573 | 5223 | 32 | 20.3 | 9.5 | 7.2 |
| BIKE-L3 | 3083 | 3115 | 10105 | 32 | 22.9 | 12.0 | 7.0 |
| Classic-McEliece-348864 | 261120 | 128 | 6452 | 32 | 1.1 | 11.9 | 4.1 |
| Classic-McEliece-348864f | 261120 | 128 | 6452 | 32 | 1.1 | 12.1 | 4.2 |
| Classic-McEliece-460896 | 524160 | 188 | 13568 | 32 | 0.9 | 13.0 | 3.8 |
| Classic-McEliece-460896f | 524160 | 188 | 13568 | 32 | 1.1 | 12.8 | 3.7 |
| Classic-McEliece-6688128 | 1044992 | 240 | 13892 | 32 | 1.2 | 14.9 | 3.6 |
| Classic-McEliece-6688128f | 1044992 | 240 | 13892 | 32 | 1.2 | 15.1 | 3.5 |
| Classic-McEliece-6960119 | 1047319 | 226 | 13908 | 32 | 1.5 | 15.6 | 3.8 |
| Classic-McEliece-6960119f | 1047319 | 226 | 13908 | 32 | 1.2 | 14.6 | 3.7 |
| Classic-McEliece-8192128 | 1357824 | 240 | 14080 | 32 | 1.3 | 17.5 | 3.6 |
| Classic-McEliece-8192128f | 1357824 | 240 | 14080 | 32 | 1.2 | 17.3 | 3.6 |
| HQC-128 | 2249 | 4481 | 2289 | 64 | 2.1 | 2.5 | 2.3 |
| HQC-192 | 4522 | 9026 | 4562 | 64 | 2.3 | 2.9 | 2.7 |
| HQC-256 | 7245 | 14469 | 7285 | 64 | 2.7 | 3.3 | 3.2 |
| Kyber512 | 800 | 768 | 1632 | 32 | 3.8 | 4.0 | 6.8 |
| Kyber768 | 1184 | 1088 | 2400 | 32 | 4.1 | 4.1 | 6.5 |
| Kyber1024 | 1568 | 1568 | 3168 | 32 | 4.6 | 4.4 | 6.3 |
| SIKE-p434 | 330 | 346 | 374 | 16 | 4.9 | 5.0 | 5.0 |
| SIKE-p503 | 378 | 402 | 434 | 24 | 1.3 | 1.3 | 1.3 |
| SIKE-p610 | 462 | 486 | 524 | 24 | 6.5 | 6.5 | 6.5 |
| SIKE-p751 | 564 | 596 | 644 | 32 | 1.3 | 1.3 | 1.3 |
| Algorithm | public key | secret key | signature | keygen/s | sign/s | verify/s |
|---|---|---|---|---|---|---|
| Dilithium2 | 1312 | 2528 | 2420 | 3.3 | 5.8 | 3.8 |
| Dilithium3 | 1952 | 4000 | 3293 | 3.5 | 5.9 | 3.6 |
| Dilithium5 | 2592 | 4864 | 4595 | 3.3 | 5.6 | 3.7 |
| Falcon-512 | 897 | 1281 | 690 | 2.6 | 19.9 | 1.0 |
| Falcon-1024 | 1793 | 2305 | 1330 | 2.3 | 21.9 | 1.0 |
| SPHINCS+-SHA256-256f-robust | 64 | 128 | 49856 | 2.1 | 2.0 | 1.0 |
| SPHINCS+-SHA256-256f-simple | 64 | 128 | 49856 | 3.1 | 2.9 | 1.1 |
| SPHINCS+-SHA256-256s-robust | 64 | 128 | 29792 | 2.1 | 2.2 | 1.0 |
| SPHINCS+-SHA256-256s-simple | 64 | 128 | 29792 | 3.0 | 3.0 | 1.0 |
6 最後に
耐量子計算機暗号は、 代表的な方式の選定やライブラリ実装を含めて、 大きく進展しているように見受けられる。 その一方で、格子暗号のみが大きく先行しているなど、 各方式が万遍なく発展しているとは言い難い現状にあると著者は感じている。 格子暗号や符号ベース暗号において、 量子計算機を用いた解析方法が提案される可能性もいまだあり得ることから、 今後は継続して格子暗号以外のさまざまな枠組みから方式を設計していくことが望ましい。 我が国においても耐量子計算機暗号の研究開発が盛んであり、 国主導のプロジェクトなども展開されている。 著者はもちろん、我が国が総力を挙げて、 今後も耐量子計算機暗号の研究開発に取り組み、 世界的な成果を上げていくことが期待される。
(大阪大学 大学院情報科学研究科 矢内直人)


